# Is Zero an Even or Odd Number? A Mathematical Inquiry
Written on
Understanding the Parity of Zero
The question “Is zero even or odd?” may seem trivial, yet its implications have historical significance. In 1977, Paris faced severe smog, leading authorities to restrict traffic based on license plate numbers—odd or even. This created confusion regarding zero's classification, highlighting its ambiguity (source).
Similarly, during Hurricane Sandy in 2012, New York City Mayor Michael Bloomberg imposed fuel rationing based on license plates, again raising the question of zero's classification. Those with plates ending in zero were categorized alongside even numbers, further complicating the matter (source). These instances prompted mathematicians to seek a definitive answer to the question of zero's parity.
What is Parity in Mathematics?
Parity refers to the categorization of integers as either even or odd. To determine this, we can pose two fundamental questions:
- How do we define an even number?
- What constitutes an odd number?
An even number is defined mathematically as follows:
“An even number is an integer of the form n = 2k, where k is an integer.”
- OEIS A005843
In essence, if an integer is divisible by 2, it is classified as even. Conversely, any integer that does not meet this criterion is considered odd. Now that we have established these definitions, let's analyze the classification of zero.
Is Zero a Multiple of 2?
An integer qualifies as a multiple of 2 if it can be expressed as 2 multiplied by another integer. For example, both 10 and 50 fit this description:
10 = 2 * 5
50 = 2 * 25
This leads to the inquiry: Is zero also a multiple of 2? Indeed, it is! Zero can be represented as:
2 * 0 = 0
This reasoning allows us to assert that zero is, in fact, even. To deepen our analysis, let’s examine certain characteristics typical of even numbers.
Divisibility by 2
All even numbers exhibit the property of being divisible by 2. This means that when an even integer is divided by 2, the remainder is zero. For instance:
4 / 2 = 2
16 / 2 = 8
In both cases, the remainder is zero. Conversely, dividing an odd integer by 2 yields a non-integer result:
25 / 2 = 12.5
Now, let’s analyze zero’s divisibility by 2:
0 / 2 = 0
Here, we also obtain an integer quotient and a zero remainder, confirming that zero adheres to the characteristics of even numbers.
Sum of Two Even Numbers
The sum of two even integers remains even. Consider these examples:
256 + 10 = 266
120 + 756 = 876
Notably, adding zero to any even number yields the same even number:
2 + 0 = 2
78865986 + 0 = 78865986
This reinforces our assertion that zero meets the criteria for the sum of two even integers.
Sum of an Even and an Odd Number
When an even number is added to an odd number, the result is always odd:
25 + 12 = 37
365 + 20 = 385
Similarly, adding zero to an odd number retains its odd status:
25 + 0 = 25
365 + 0 = 365
Thus, zero satisfies this condition as well.
Subtracting 2 from Even Numbers
Subtracting 2 from an even number results in another even number. Starting with 8:
8 – 2 = 6
6 – 2 = 4
4 – 2 = 2
Continuing downward:
2 – 2 = 0
0 – 2 = -2
-2 – 2 = -4
Here, we see that zero seamlessly fits within the framework of even numbers without contradiction.
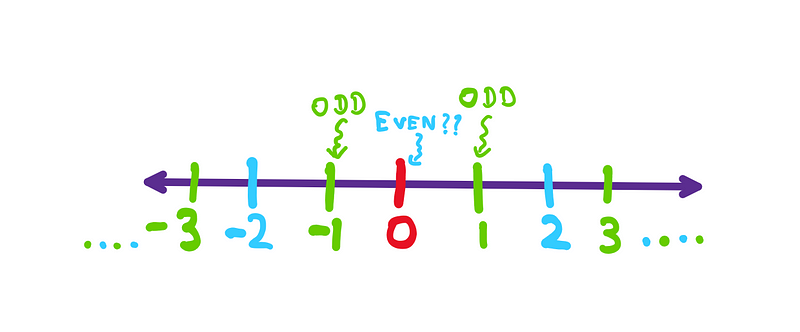
The Position of Zero on the Number Line
On the number line, every even integer is flanked by odd integers. Notably, zero is positioned between -1 and 1, reinforcing the concept of its evenness.
Conclusion
Through our analysis, it is evident that zero meets the mathematical criteria for being classified as an even number. However, real-world scenarios, such as in roulette, treat zero differently, categorizing it as neither even nor odd. Despite this, from a mathematical standpoint, zero is indeed even.
As we look to the future, it would be advantageous to achieve consensus on the classification of zero in various contexts.
If you found this exploration engaging, consider supporting my work by following and subscribing. For further reading, you may explore topics such as "What Really Happens When You Divide By Zero?" and "Does Division By Zero Really Lead To Infinity?"