Optimality of the Powers of 3 Strategy in Weighing Scale Puzzles
Written on
Chapter 1: Introduction to the Weighing Scale Puzzle
In the earlier discussion, we examined Hemanth’s method for solving the weighing scale puzzle and established its general applicability. To summarize: it is indeed possible to measure any positive integer weight using only weights that are powers of 3.
Now, the question arises: is this "powers of 3" approach the most efficient? Specifically, can we demonstrate that no alternative strategy requires fewer weights?
As pointed out by Hemanth, a set of n known weights generates 3^n combinations since each weight can be placed in three positions: on the left pan, on the right pan, or not used at all.
Among these combinations, one will always yield a weight of 0. Consequently, we are left with 3^n - 1 "interesting" combinations. However, it is important to note that half of these can be negative (if excess weight is placed on the right pan).

Chapter 2: Proving the Optimality
The combinations produced by weights are not necessarily unique. For example, having weights of 2 kg, 3 kg, and 5 kg allows you to achieve the same result by either placing the 5 kg weight on one side or by using the 2 kg and 3 kg weights together.
This leads to the hypothesis that a strategy which can weigh every positive integer weight and produces solely unique results must be optimal. In previous discussions, including Hemanth’s original post, we confirmed that the powers of 3 can weigh any object—now we must verify if they yield only unique results.
The answer is affirmative, and the proof follows directly from the inductive reasoning previously utilized. Here’s how it unfolds.
Starting with the first k powers of 3, the smallest combination achievable is 1 (3^0). Our inductive reasoning has already established that we can generate every integer from 1 up to the maximum combined weight possible, which is...
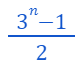
This leads to a specific list of weights we can measure:
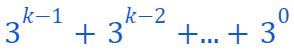
Thus, we have precisely...
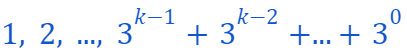
Furthermore, we know that the first k powers of 3 can create...
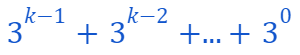
If each combination corresponds uniquely to one of the possible weights, we can conclude that the powers of 3 strategy is indeed optimal.
To illustrate, if...
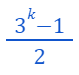
Then the powers of 3 strategy is optimal. Conversely, if...
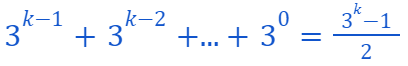
This indicates that at least one number from our list can be formed through multiple combinations.
Let’s employ mathematical induction to further solidify our claim.
Proof by Mathematical Induction
We aim to prove the statement:
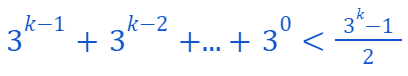
for any k > 0.
Base Case
In our base case, we need to demonstrate that P(1) holds true.
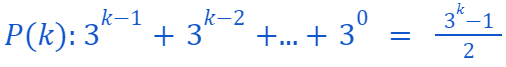
Indeed, P(1) is valid.
Inductive Step
Assuming P(n) is true, we must show P(n + 1) also holds.
Assuming P(n), we know...
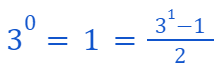
We need to demonstrate that...
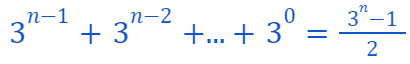
By our assumption, we find...
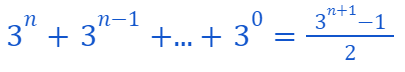
Combining these terms into a single fraction yields:
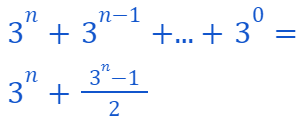
Thus, we have established that given...
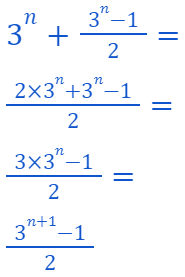
It follows that...
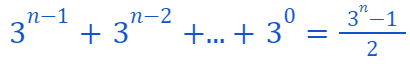
This confirms our inductive step is complete!
Consequently, our proof asserts that...
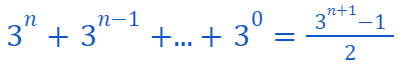
holds true for any k > 0.
Q.E.D.
Engaging Video Resources
To further enhance your understanding of these concepts, here are two videos:
The first video titled "Can you solve the classic 12 marbles riddle? (Detailed Solution Video)" elaborates on similar puzzle-solving techniques.
The second video, "Pan balance with a 'double scales' - puzzle problems for 4th grade and up," provides insights into practical applications of weighing puzzles.