Exploring the Minimum Infinite Sum: A Fun Algebra Challenge
Written on
Understanding Infinite Sums
Recently, I ordered from Pret A Manger via UberEats, and the price was surprisingly high! However, I must refocus on my writing to fund my occasional food cravings.
Before diving into the solution, remember that S must be a positive value. I suggest you take a moment to pause this article, get your pen and paper, and attempt the problem yourself. Once you’re ready, continue for the solution!
Solution Overview
Let’s denote the common ratio of the geometric series as r. Given that the second term equals 1, it follows that the first term can be expressed as 1/r. We can start writing the series terms as follows:
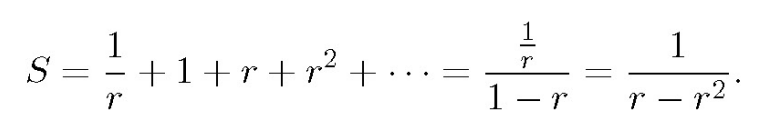
In this context, we apply the formula S = a/(1 - r), where a represents the first term, and r is the common ratio. For our scenario, we have a = 1/r, as shown previously.
Simplifying this expression results in:

Notice that since S > 0 and S is equal to 1/(r - r²), we can minimize S by maximizing the expression r - r². This allows us to reframe our problem as one concerning a downward-opening parabola, f(r) = r - r².
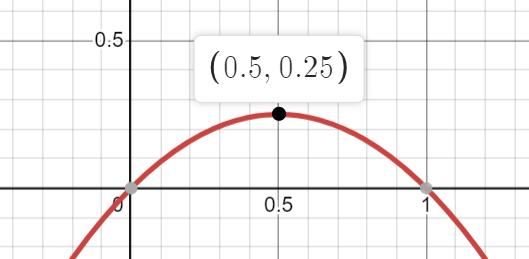
The vertex of this function occurs at (0.5, 0.25), indicating that 0.25 is the peak value. You could also arrive at this conclusion through methods such as completing the square or taking the derivative. Therefore, the smallest possible value for S is:

And that concludes our solution.

What are your thoughts on this problem? I’d love to hear your insights in the comments below!
Don't forget to save and share the following collection of intriguing math puzzles on Medium:
Math Puzzles Collection
The best math puzzles covering Algebra, Geometry, Calculus, Number Theory, and more. Share these with your friends to challenge their minds!
Bella’s Weekly Math Challenges
Join the 48-hour weekly math competition for exciting challenges!
Thank you for reading! If you found this article helpful, please give it a clap.

If you appreciate my work, consider buying me a coffee. Your support means the world to me as I continue my writing journey. Happy Solving, Bella 😊
Chapter 2: Video Insights on Infinite Sums
In this chapter, we will explore two insightful videos to deepen our understanding of infinite sums.
The first video titled "Infinite Series: Minimum Number of Terms for a Given Accuracy" provides an excellent explanation of the topic.
The second video, "13.2 The Definition of Infinite Sum," further elaborates on this fascinating subject.