# Exploring Finite Approximations: Mathematics in Engineering Design
Written on
Understanding Finite Approximations
Have you ever wondered how modern aircraft, like the Boeing 747, are designed to remain airborne? The complexity of crafting such sophisticated machines far surpasses the simpler designs of the Wright brothers. A key challenge lies in conceptualizing the wings so they withstand the forces acting upon them during flight. Engineers do not rely solely on trial and error, as this would be prohibitively expensive. Instead, they utilize computer simulations to create and test the components of the aircraft in a virtual environment. This article delves into the processes behind these simulations.
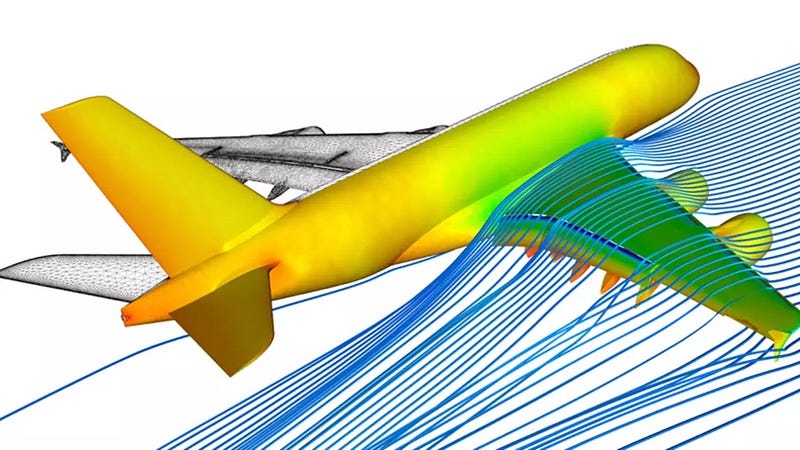
In the context of aviation, these simulations are known as Computational Fluid Dynamics (CFD). Many software solvers exist to facilitate such analyses. Regardless of the solver used, they all share two foundational elements: they address partial differential equations and rely on finite approximations.
To grasp the concept of finite approximations, we must dissect the term. “Finite” refers to working with minute segments of a larger whole. By zooming in on a vast entity, we can simplify its complexities; for instance, while the Earth is spherical, the ground beneath our feet appears flat. This linear perspective is easier to represent mathematically. In essence, finite approximations are mathematical algorithms that define minuscule segments of a physical process or structure. By compiling numerous finite “elements,” we aim to accurately model the real-world phenomena.
In this discussion, we will explore three widely used finite methods: The Finite Difference Method, The Finite Volume Technique, and The Finite Element Method. Each of these approaches has its unique advantages and limitations, starting with the Finite Difference Method.
Finite Difference Method Overview
When examining a particular physical process, such as electron movement, we can apply the finite difference method by partitioning our domain into numerous points, forming a grid.
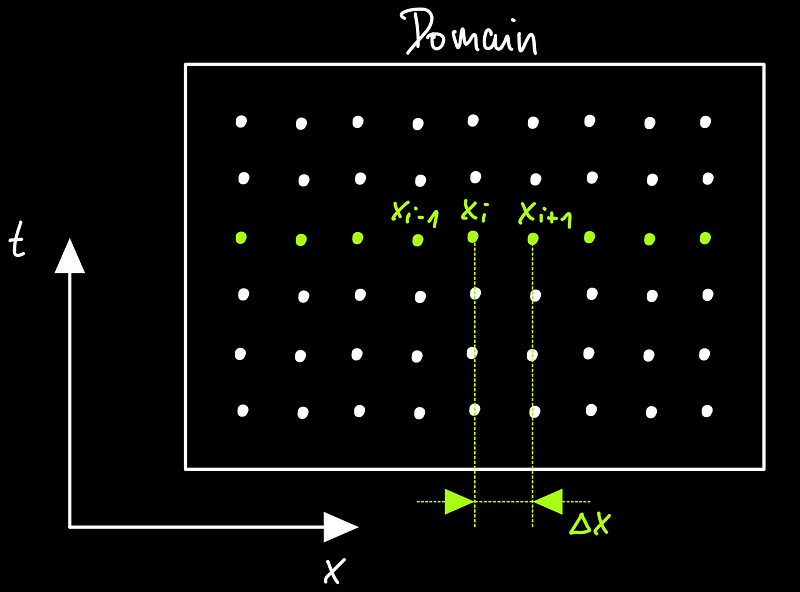
To simplify, let’s consider a one-dimensional problem where each point represents data relevant to our physical model. By indexing these points with the letter ‘i,’ we can establish a reference point and calculate the backward difference as follows:
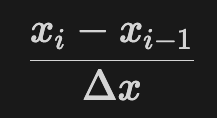
Next, we can derive the forward difference:
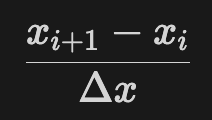
Lastly, we can compute the central difference:
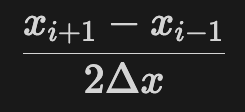
This process employs two points, subtracting one value from another and dividing by the distance separating them. The accuracy of our results hinges on how closely spaced these points are, presenting a challenge inherent in finite approximations.
You may be wondering, "What distinguishes the different difference methods?" Depending on the physical problem at hand, one method may exhibit greater stability, which is crucial for time-dependent simulations. Although the finite difference approach seems straightforward, it encounters limitations when addressing complex geometries, such as circular domains.
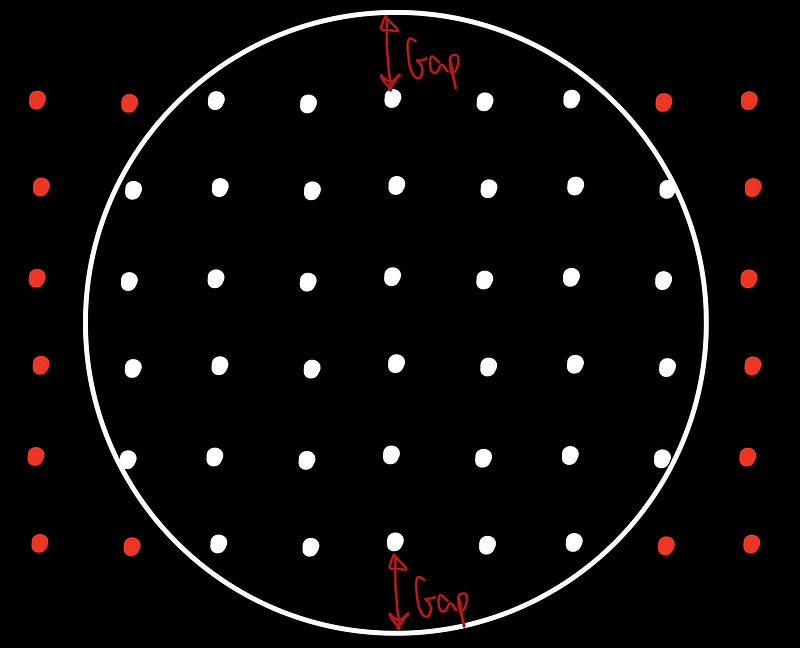
This is where the Finite Element Method (FEM) becomes beneficial.
Finite Element Method
Unlike the finite difference method, which relies on discrete points, the Finite Element Method employs finite elements for analysis. To illustrate, let’s focus on a circular domain where finite difference struggles. By using triangular elements, the FEM can represent the same domain more accurately.

Each triangular element comprises nodes that hold the values representing our physical problem. However, managing these nodes introduces complexity. Each element shares nodes with adjacent elements, ensuring continuity.
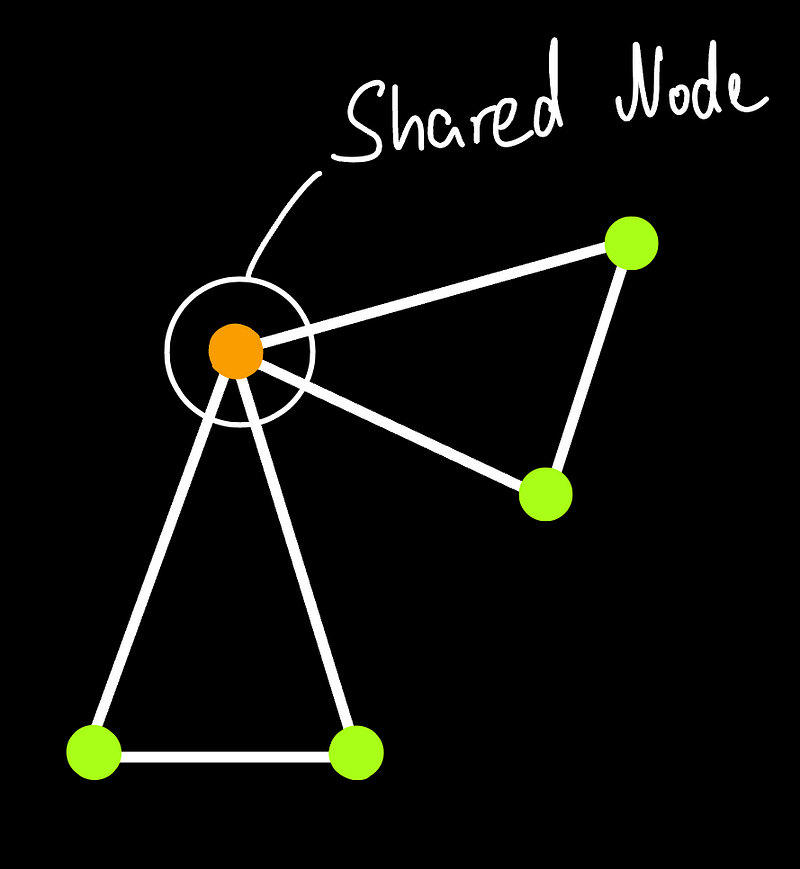
Computing these nodes is more challenging than in the finite difference method, warranting a deeper exploration in future discussions. Nonetheless, the FEM excels at modeling intricate geometries, albeit at the cost of increased computational demands.
Finite Volume Technique
The Finite Volume Technique is employed when addressing problems related to the flow of mediums, such as the conservation of mass and energy. This approach divides the physical problem into small volumes, aiming to determine the flux within each volume to collectively represent the system's behavior.
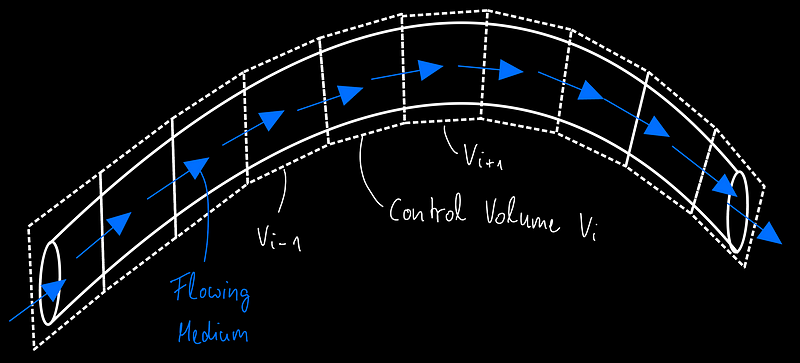
While this method offers robust solutions, it often involves complex integrals, making it one of the most challenging techniques. My current research, involving the Discontinuous Galerkin method, merges FEM principles with numerical fluxes from the Finite Volume Scheme. Further details will be covered in future posts, so stay tuned.
The first video, titled "Finite Difference Approximations," provides insights into these methods and their applications in engineering design.
The second video, "Estimating Area with Riemann Sums Finite Rectangles Calculus 1 AB," offers a foundational understanding of Riemann sums, relevant for understanding finite approximations.
Thank you for exploring this topic with me. If you found this information valuable, consider subscribing to my newsletter, "The Creative Engineer," or following my work for more insights into engineering and mathematics. Your feedback is welcome, so feel free to reach out with any questions or comments!