Chapter 1: Introduction to Generalized Additive Models

The Generalized Additive Model (GAM) is a regression framework in machine learning that emerged in the 1990s. Its structure bears resemblance to multiple linear regression models.

(Baayen, R. H. and M. Linke (2020). “An introduction to the generalized additive model.” A practical handbook of corpus linguistics. New York: Springer: 563–591.)

For further details on linear regression, refer to the section below:

The primary distinction between GAMs and traditional regression models is that GAMs do not presuppose a linear correlation between independent and dependent variables.

(Hastie, T. and R. Tibshirani (1987). “Generalized additive models: some applications.” Journal of the American Statistical Association 82(398): 371–386.)

The equation to formulate a GAM regression is expressed as follows:

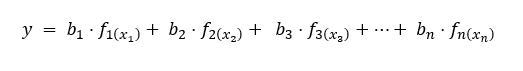
Here, f1, f2, f3, …, fn are termed smooth functions, which depict a continuous curve that illustrates the relationship between the dependent variable and the independent variables x1, x2, x3, …, xn.

(Baayen, R. H. and M. Linke (2020). “An introduction to the generalized additive model.” A practical handbook of corpus linguistics. New York: Springer: 563–591.)

These smooth functions are estimated using splines, a flexible approach for capturing nonlinear relationships between variables. Splines consist of piecewise-defined polynomials and are widely utilized in mathematics and engineering for approximation and interpolation. They are specifically selected to represent the data accurately while minimizing model complexity.

(Ma, S. (2012). “Two-step spline estimating equations for generalized additive partially linear models with large cluster sizes.” The Annals of Statistics 40(6): 2943–2972, 2930.)

The initial GAM fitting method estimated the model's smooth components using non-parametric smoothing through the backfitting algorithm. This technique iteratively smooths partial residuals, allowing for modular estimation that can incorporate various smoothing techniques for the fn(xn) terms. However, a limitation of backfitting is its often inadequate integration with the smoothness estimation of modal terms, frequently requiring manual user adjustments or selections from a limited number of predefined smoothing options.

When utilizing smoothing splines, the smoothness degree can be integrated into the model via generalized cross-validation or restricted maximum likelihood, capitalizing on the relationship between spline smoothers and Gaussian random effects. This comprehensive spline approach entails computational challenges, particularly as n, the number of observations for the dependent variable, increases, which can make it impractical for larger datasets.

To gain insights into evaluating the results from fitting functions to data points, you might find this article helpful, which elaborates on seven different metrics:

How to Train Generalized Additive Models (GAMs) in Model Studio - YouTube

This video provides a detailed guide on training GAMs within a model studio setting, demonstrating practical applications and techniques.

Chapter 2: Understanding the Application of GAMs

Introduction to Generalized Additive Models with R and mgcv - YouTube

In this video, an overview of GAMs using R and the mgcv package is presented, exploring their implementation and benefits in statistical modeling.

Conclusion

In summary, the Generalized Additive Model (GAM) stands out as a regression model that departs from the assumptions of linear relationships inherent in traditional linear regression. By employing smooth functions (f1, f2, f3, …) to capture intricate, nonlinear interactions, GAMs leverage splines for effective data representation. The original fitting method utilizes backfitting, which, while versatile, may necessitate manual adjustments. When smoothing splines are involved, the smoothness can be incorporated through cross-validation or maximum likelihood, albeit at a computational cost, especially for larger datasets.