Mastering a Challenging Algebra Equation: A Comprehensive Guide
Written on
Chapter 1: Introduction to the Algebra Challenge
Welcome to the third installment of our series on complex algebraic problems. At first glance, the equation we’re tackling might seem daunting. Unlike previous equations, I must admit that this one truly presents a challenge!
It’s worth noting that while I’ve labeled this as an algebra problem, solving it demands skills beyond mere algebraic manipulation. But don't worry, I’ll be transparent about this!
Spoiler Alert:
If you're feeling adventurous and want to attempt the problem independently, I encourage you to do so now. You can return to this discussion once you’ve given it a shot. The subsequent sections will delve into the solutions for this equation.
Section 1.1: A Basic Strategy for Tackling the Algebra Problem
As previously mentioned, my first instinct when dealing with equations that feature unknown exponents is to tackle the exponents head-on. The logarithmic function often proves useful for this purpose. Let's explore what unfolds when we employ this strategy.
Math illustrated by the author
Here, we observe the expression x/log(x) on one side and y/log(y) on the other. The situation may appear grim, but it’s not entirely hopeless. We can evaluate various values of ‘x’ and ‘y’ and plot their respective output functions on a Cartesian plane.
The intersection points of these graphs will correspond to the solutions of the equation. However, there are several drawbacks to this method:
- Countless pairs of ‘x’ and ‘y’ exist for consideration.
- Graphing requires considerable resources.
- The logarithmic function isn't necessary for this task; we could work directly with the original equation.
Given these limitations, it seems prudent to shift to a more sophisticated approach to derive a general solution.
Section 1.2: A More Advanced Method to Solve the Algebra Equation
One critical insight is understanding that x^y represents ‘x’ multiplied by itself ‘y’ times, and y^x signifies ‘y’ multiplied by itself ‘x’ times.
Math illustrated by the author
This implies that either ‘x’ is a multiple of ‘y’ or vice versa. To solve the equation effectively, we can leverage this relationship and formulate a new equation. For example, we can express ‘y’ as a multiple of ‘x’.
Math illustrated by the author
In this context, the factor ‘t’ serves as a parameter that can assume any real number value. Notably, ‘t’ operates independently of both ‘x’ and ‘y’. By presenting ‘y’ as a multiple of ‘x’ through the parameter ‘t’, we have constructed a new equation.
In mathematics, such a formulation is termed a parametric equation, commonly utilized in applied mathematics and engineering. For instance, a parametric equation describing a circle can be expressed as:
x = r cos(t)
y = r sin(t)
With the new parametric equation established, we can now approach the problem from an algebraic perspective.
Chapter 2: Solving the Algebra Problem
Now, I will substitute the parametric value of y (which equals tx) into the original equation and take the x-th root on both sides of the resulting equation:
Math illustrated by the author
Next, I will manipulate the equation to express ‘x’ solely in terms of ‘t’.
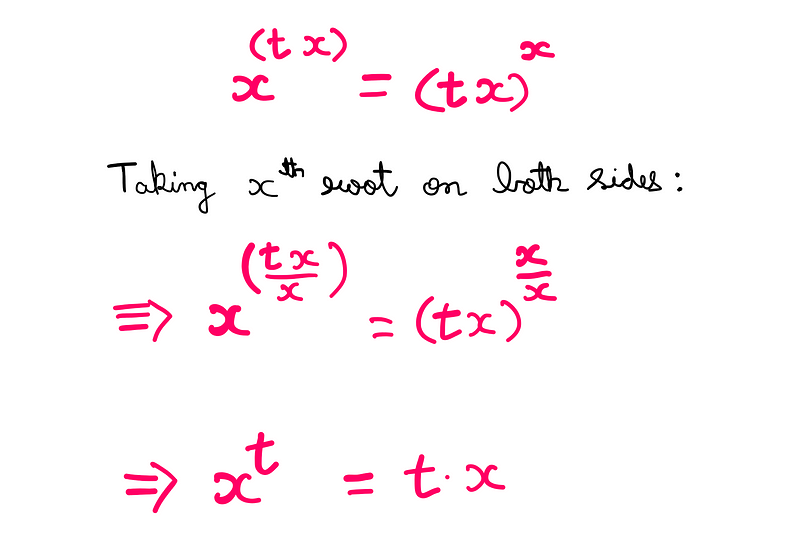
Math illustrated by the author
We can continue by multiplying by t^(1/t) and dividing by x^(1/t) on both sides, leading to:
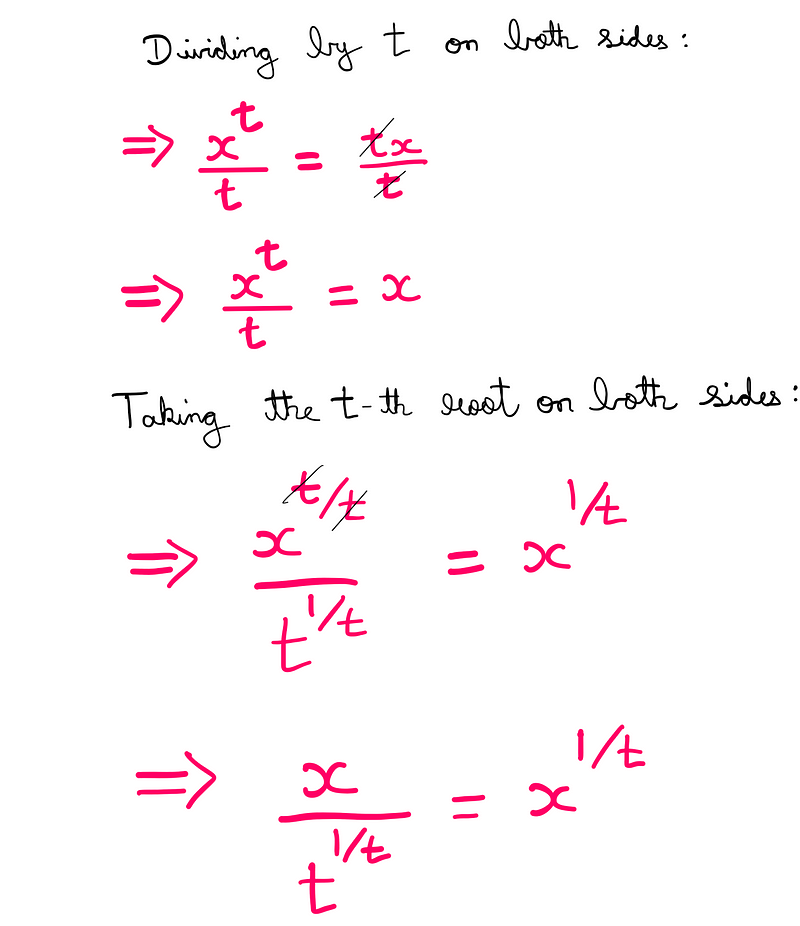
Math illustrated by the author
At last, we have an equation that expresses ‘x’ exclusively in terms of ‘t’, which was my original aim.
Section 2.1: Conclusion and Insights
We’re nearing the finish line. The final step involves plugging this equation back into the initial parametric equation to derive ‘y’ solely in terms of ‘t’ as well.

Math illustrated by the author
Consequently, we can articulate our solution to the original equation as a set of parametric equations:
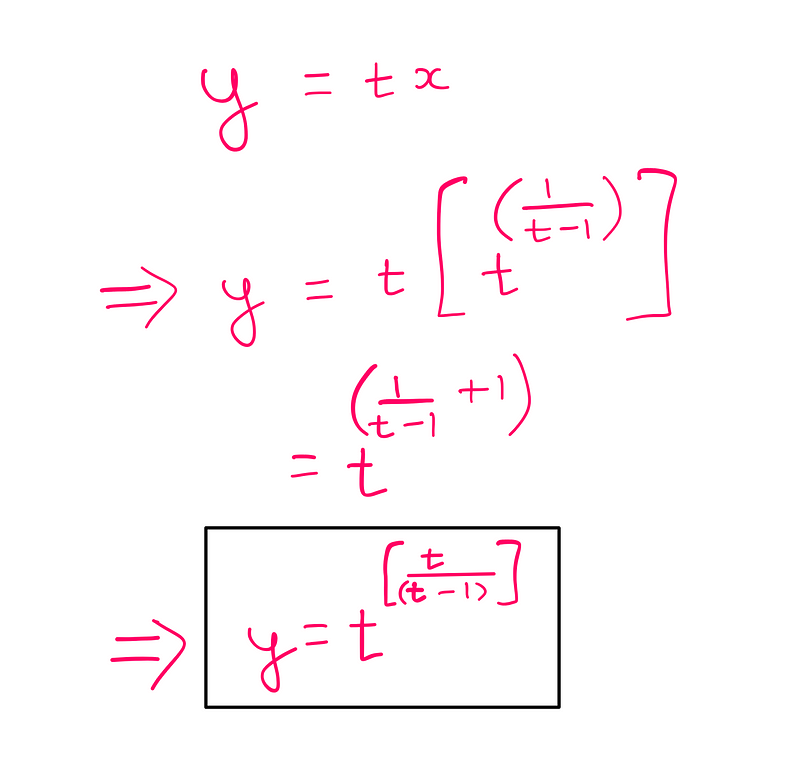
Math illustrated by the author
There are a few final considerations to address. When t=1, we encounter a scenario where the exponent for both x and y is 1/0, which is undefined in mathematics (for more on this, refer to my discussion on division by zero). Similarly, when t=0, we face 0?, which is also undefined for different reasons (explore my essay on zero raised to the power of zero for details).
To maintain our solution within the realm of real numbers (and avoid delving into complex numbers), we should restrict the values of t to: t > 0 and t ≠ 1 (as t=0 and t=1 lead to undefined states).
Sample Calculations for the Algebra Equation
To validate our findings, let’s consider ‘t = 4’:
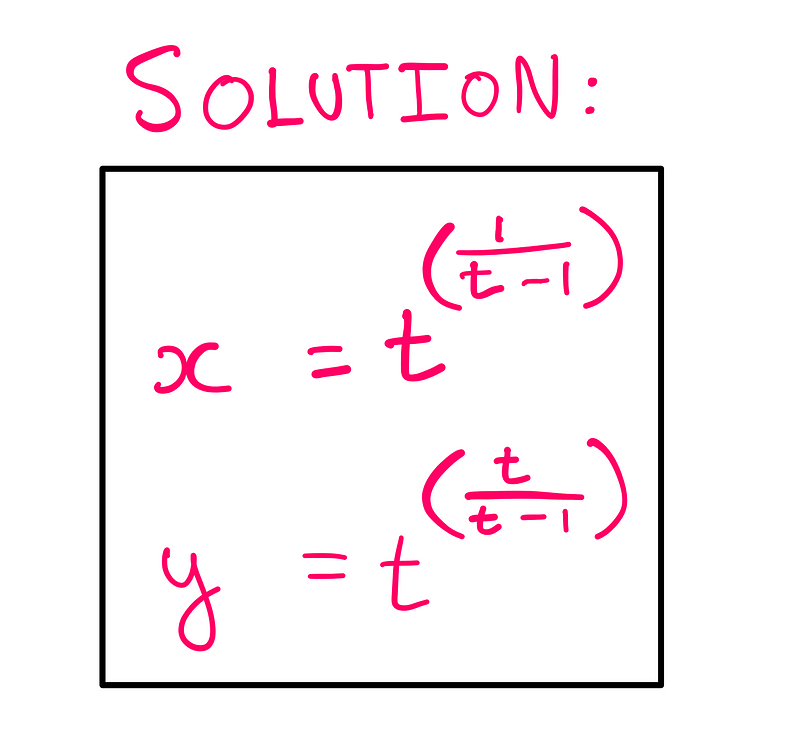
Math illustrated by the author
As demonstrated, our set of parametric equations holds true for any real value of t (within the stipulated constraints), encompassing both rational and irrational numbers.
To explore an intriguing alternative method of solving this problem using logarithms (which I initially struggled with), check out Hein de Haan’s article.
For further reading, you may find interest in: How To Really Solve This Tricky Algebra Problem? and How To Really Solve i^i?
If you’d like to support my work as an author, please consider contributing on Patreon.
This video explores a challenging math problem, encouraging viewers to think critically and engage with the material.
In this video, the presenter tackles an extremely difficult viral math problem, showcasing various methods and strategies for finding a solution.