Exploring the 2024 Mongolian Mathematical Olympiad Challenge
Written on
Chapter 1: Introduction to the Problem
Have you tackled this intriguing challenge from the 2024 Mongolian Mathematical Olympiad? At first glance, it may appear quite tricky, but with some contemplation, you might find it more manageable than expected. Before diving into the solution, take a moment to give the problem a thorough attempt.
In problems of this nature, the crucial insight often revolves around divisibility, and this one is no exception. Let’s first examine the prime factorization of 2024: 2024 = 2³ · 11 · 23. We notice the interesting factor of 2³ in our expression. If c is an even number, then it follows that 2 must divide c². As a grows larger, it too will become divisible by 2. With b being less than a, we can conclude that for sufficiently large a, there will be no solutions. It's worth noting that 2 divides 6!, which implies that a must be at most 5.
Now, you might ask why we only consider the scenario where c is even. The reason is that since c² is non-negative, it follows that a! + b! must equal 2024. The left-hand side can only be odd if one of a! or b! is odd, but since b < a, we must set a = 1. If a = 1, b must be relatively large (at least 7, given that 6! = 720), and analyzing the equation modulo 3 reveals inconsistencies. Given that c² is a square, if it were an odd square, it would then be congruent to 1 mod 3, which is not feasible. Hence, c must indeed be even.
We have already examined the case when a = 1, and similar reasoning applies to a = 2, 3, and 4 when considering them under mod 4 or mod 3. The last case to evaluate is when a = 5. Setting a = 5 leads us to the equation 720 + b! = c² + 2024, which simplifies to b! = c² + 1904. As noted, b must be at least 7. Clearly, b = 7 yields no solutions, while b = 8 results in a singular solution (5, 8, 14). What about other potential solutions? We will demonstrate that none exist.
Chapter 2: Analyzing the 2-adic Valuation
Introducing new notation, we define the p-adic valuation of an integer as the highest power of the prime p that divides it. Let’s now assume b ≥ 9. The prime factorization of 1904 is 2⁴ · 7 · 17, indicating that the 2-adic valuation of 1904 is 4. If the 2-adic valuation of c is at least 2, we arrive at the following:
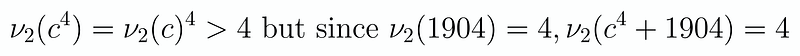
Consequently, the 2-adic valuation of b! must also be 4. This scenario can only occur if b = 6 or b = 7. This leads us to a contradiction, meaning the 2-adic valuation of c must be 1.
We can express c as c = 2k for some integer k. This transforms our equation into b! = 16k² + 1904 = 16(k² + 119). However, k cannot be even; otherwise, the 2-adic valuation would exceed 2. Despite this, the 2-adic valuation of b! remains greater than 4, necessitating that 2³ divides k² + 119. This presents a contradiction since it would require an odd square to equal 1 less than a multiple of 8, which cannot hold. Thus, we confirm that the only solution found earlier stands as the sole answer:
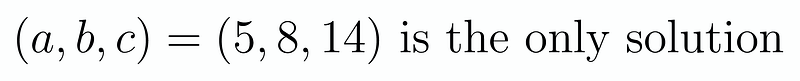
Did you enjoy this analysis or discover something new? If you did, consider supporting my work—it means a lot! Have you come across a different solution or have suggestions for a new problem? Don’t hesitate to share your thoughts in the comments!