Understanding the Power Rule: A Fresh Perspective on Calculus
Written on
Chapter 1: Introduction to the Power Rule
This section presents a derivation of the power rule that diverges from the traditional limit-based approach taught in Calculus I. Drawing from Abraham Robinson's concepts of non-standard analysis and hyper-real numbers, we will demonstrate a fresh method of understanding this foundational calculus principle.
The conventional derivation of the power rule typically begins with a definition of the derivative. Here, we will instead employ infinitesimals, allowing you to choose the method that resonates more with your understanding.
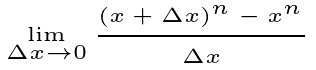
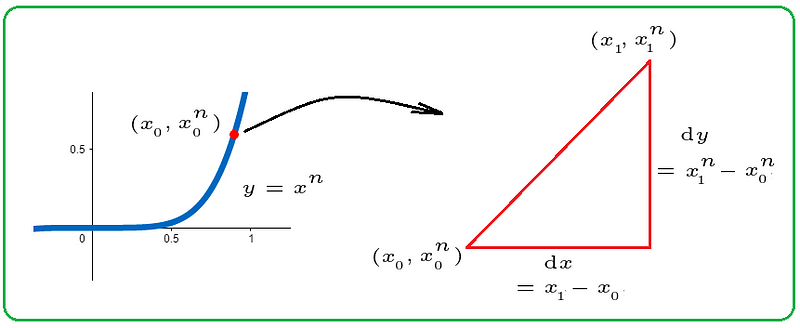
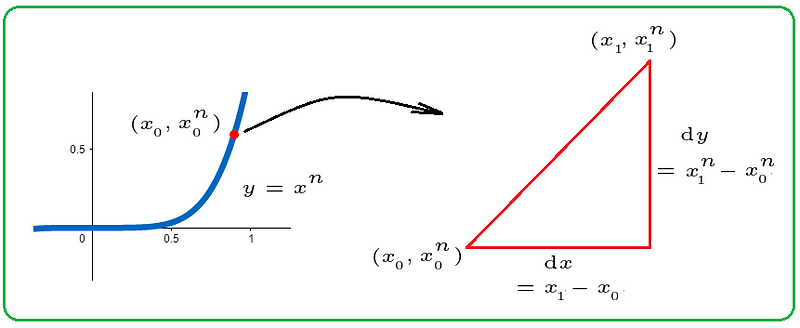
As illustrated, we start with a general power function of degree n, where the coefficient is set to 1 for simplicity. This derivation can be easily adapted to accommodate any coefficient.
What is the slope of the function at the specified point depicted on the left side of the diagram? The right side provides an infinitely magnified view of this point, revealing a neighboring point that is exceedingly close to our point of interest. The slope of the line connecting these two points is calculated below.
Continuing with specific cases—n=2 and n=3—we will search for a pattern that allows us to generalize.
Section 1.1: Analyzing Specific Cases
For the case where n=2:
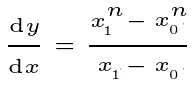
The two values forming the sum at the conclusion are infinitely close to each other. Therefore, we can simplify our expression:
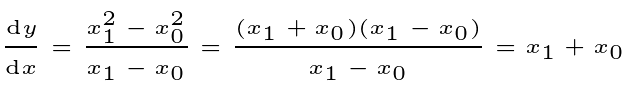
The resulting expression combines a finite term (2x?) with an infinitesimal (dx), allowing us to disregard the infinitesimal in our final result.
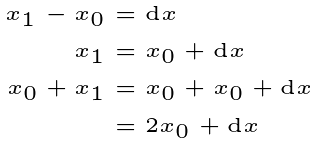
For n=3:
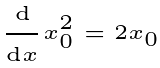
We can apply reasoning similar to that of n=2 to the initial part of this expression.
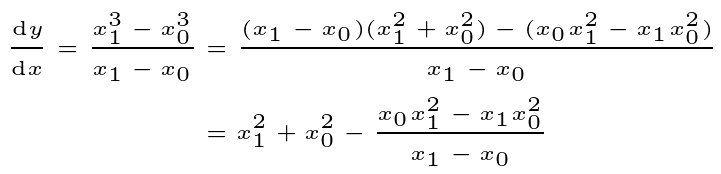
Next, we address the rational expression beside it.
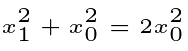
We will resolve the product at the end alongside the infinitesimal, dx.
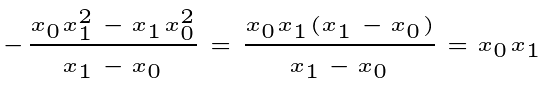
The last operation involves multiplying by the infinitesimal, yielding a result akin to multiplication by zero. Ultimately, we combine the two results.
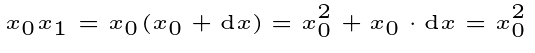
Once more, this aligns with our anticipated outcome.
Chapter 2: Generalization of the Power Rule
While we could conclude our exploration here, we will instead pursue a more comprehensive general formula utilizing infinitesimals.
By comparing the two specific cases discussed, we notice that each involves division by (x?-x?), effectively reducing the exponent by 1. In the case of n=3, we perform this operation twice.
The identity for the difference of two squares is as follows:
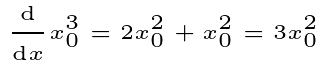
I encourage you to verify the following:
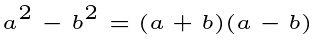
We can extend this reasoning to any integral exponent. Consider two numbers, a and b, such that:
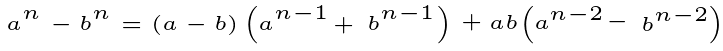
In this context, ? represents an infinitesimal. While zero is also infinitesimal, ? is a larger quantity!
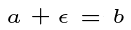
Multiplying by ? results in 0.
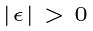
We will continue dividing in the same manner.
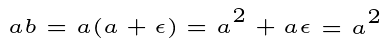
Next, we again address the rational expression.
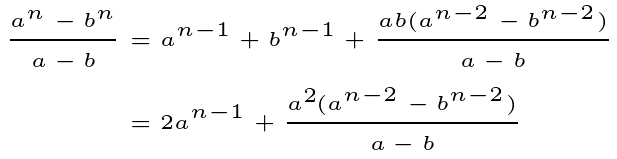
Focusing on the first part of this expression yields:
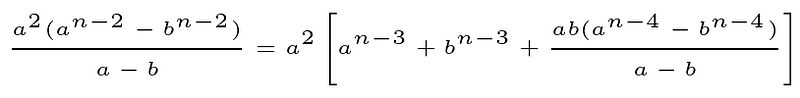
With each iteration, this expression continues to produce:
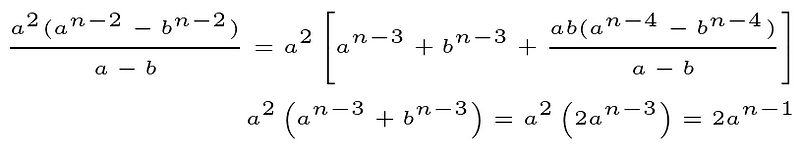
After going through this process twice, we can summarize our findings.
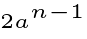
If n is even, we can complete ½ n iterations, leading us to:
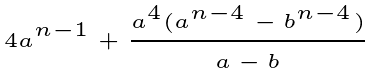
If we can eliminate the rational expression entirely, we will conclude our derivation (for n even).
The numerator simplifies to 0, while the denominator, although infinitesimal, remains greater than zero. This has always been permissible within our framework.
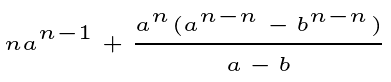
Lastly, when n is even:
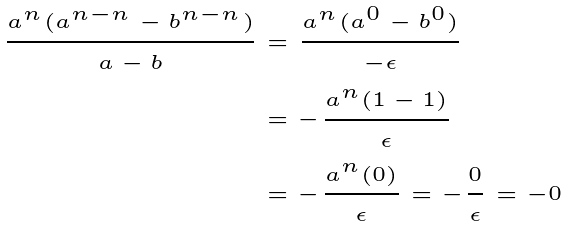
What about when n is odd?
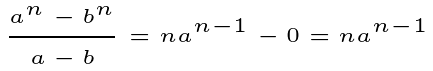
In this scenario, we can perform ½ (n -1) iterations, leading to:
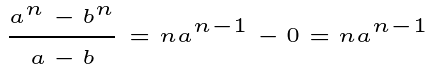
An Historical Note
In the 19th century, Cauchy introduced rigor to calculus through his theory of limits, which remains the foundation of most contemporary calculus textbooks. In the mid-20th century, Abraham Robinson advanced non-standard analysis, which utilizes infinitesimals—numbers that are non-zero yet infinitely small.
Further Exploration
- An Introduction to Non-Standard Analysis — A technical paper for deeper insights.
- Calculus Made Easy — Silvanus Thompson’s work presents differentials with a refreshing take on the power rule.
- Elementary Calculus: An Infinitesimal Approach — This text provides a more rigorous examination, introducing hyper-real numbers as an extension of real numbers.
The video titled "Dual complex numbers and Leibniz's differentiation rules | Famous Math Problems 22b | N J Wildberger" delves into complex numbers and their implications for differentiation, providing valuable context to our discussion.
Additionally, "Newton's Infinitesimal Calculus (4): Calculating Fluxions/Derivatives" provides further insights into the historical context and techniques surrounding infinitesimal calculus.