What Makes Special Functions Unique?

You might wonder what exactly distinguishes special functions from more commonly known functions like sines and cosines. The term "special" can be misleading, as it doesn't imply superiority. Instead, it seems to stem from the fact that these functions are seldom covered in high school curricula. While they may not be essential for basic applications in high school science, they become increasingly relevant in advanced college-level studies. Unfortunately, many students tend to halt their exploration of new functions after high school, relying on lookup resources rather than developing a deeper understanding. I argue that it’s crucial to familiarize oneself with the fundamental properties of special functions. Just as with trigonometric functions, where only a few key properties are typically needed for most applications, the same principle applies to special functions.

Recognizing the Gamma Function

The most critical aspect of working with any special function, including the Gamma function, is the ability to identify it when it appears in calculations. The Gamma function frequently shows up in integral form, defined as follows:

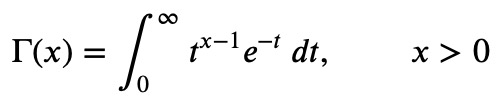
Memorizing this definition is beneficial, as it often simplifies your work by allowing you to utilize the properties of the Gamma function instead of dealing with the integral directly.

Connection to Factorials

The Gamma function has a close relationship with factorials. For any positive integer n, it can be expressed as:

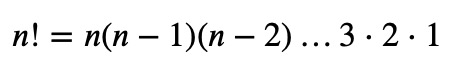
This relationship is worth remembering. To illustrate this connection, consider the following integral:

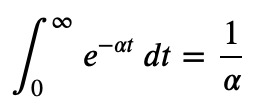
Differentiating this equation with respect to a variable and simplifying leads to the important conclusion:

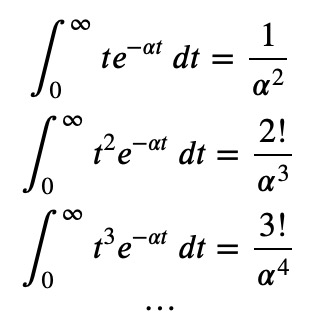
Setting the variable equal to 1 helps clarify why (0! = 1) when solving the corresponding integral.

Recursion Formula

A key property of the Gamma function is its recursion formula:

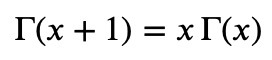
This can be demonstrated through integration by parts on the integral representation of (Gamma(z + 1)). It's also an excellent opportunity for you to practice identifying the Gamma function in various contexts, so consider proving this yourself!

Defining for Negative Arguments

Until now, we have only discussed the Gamma function for real numbers greater than zero. However, it can be extended to negative values. Since the integral representation does not apply here, we can utilize the recursion relation as a new definition:

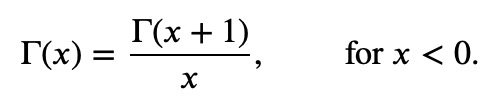
This allows us to derive (Gamma(z - 1/2)) from (Gamma(1/2)):

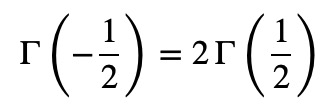
Key Values to Remember

For positive integers, the Gamma function equates to the factorial. Conversely, for negative integers or zero, the Gamma function approaches infinity. One of the most crucial values to remember is (Gamma(1/2)):

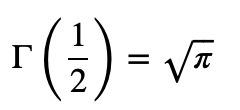
This value is particularly important as it often appears in practical applications involving integer or half-integer arguments. Knowing (Gamma(1/2)) allows you to simplify expressions involving factorials and powers of pi.

Summary Cheat Sheet

For your convenience, here’s a summary of essential properties to remember: