Understanding Game Theory: Utility and Zero-Sum Games Explained
Written on
Chapter 1: The Concept of Utility
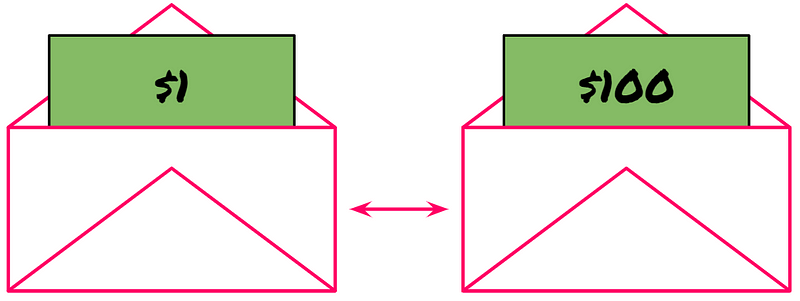
Consider this scenario: I present you with a choice between receiving $1 or $100. Which would you select? (It's straightforward.)
A Simple Decision
Naturally, you would choose $100 because it holds greater value than $1. This illustrates the basic notion of utility.
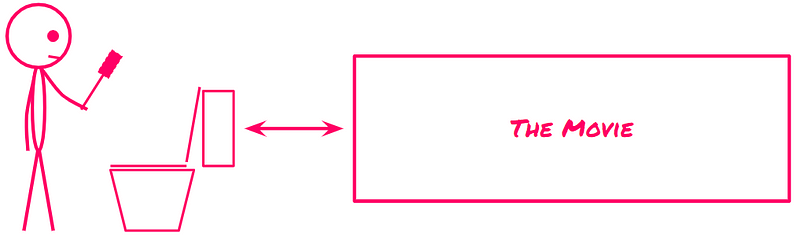
Now, what if I offered you a decision between watching a movie and cleaning a restroom?
Another Obvious Choice
While personal preferences play a role, most individuals would prefer watching a movie. In this case, the utility of going to the movies surpasses that of cleaning a restroom. Just as temperature indicates how hot something is, utility quantifies how appealing an option is.
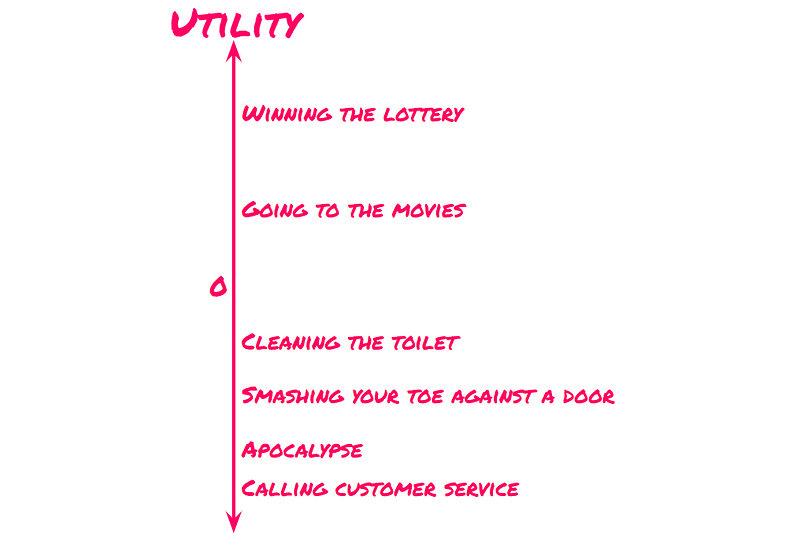
Utility varies from person to person. For instance, I might find joy in reading a science book, while others may view it as a waste of time. Now, let's delve into a more intriguing example: Tic Tac Toe.
Chapter 2: Analyzing Tic Tac Toe
Tic Tac Toe is a simple game that consists of a 3x3 grid with nine empty squares:

In this game, two players alternate turns, marking one of the empty squares. One player uses "X," while the other uses "O." The objective is to be the first to align three of your marks either horizontally, vertically, or diagonally.

Tic Tac Toe exemplifies a zero-sum game. A victory for one player results in an equivalent loss for the other—when one player achieves three in a row, the opponent inevitably loses. However, a game can end in a tie if all squares are filled without a winner.
Let’s take a closer look at a standard game of Tic Tac Toe:
Player X starts by marking the top left corner:
Player O may respond by marking:
The game progresses as follows:
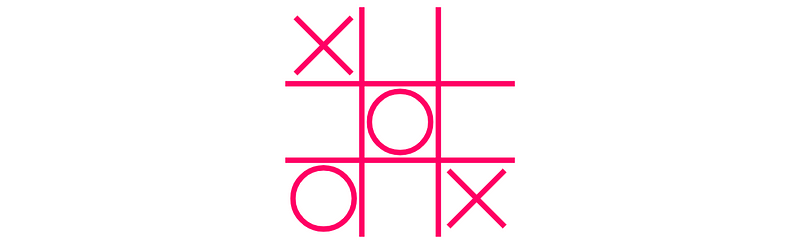


In this sequence, Player X ultimately wins. But how does one decide which move to make?
In the second-to-last position, Player X had three potential moves (indicated by numbers 1, 2, and 3):
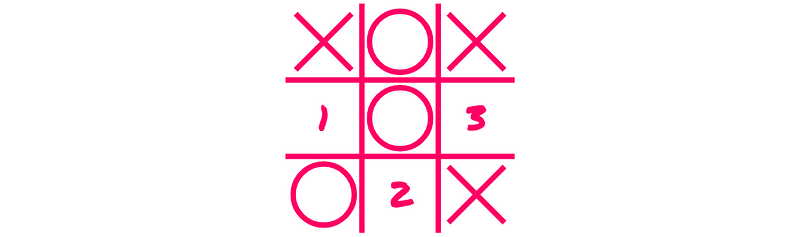
Move 1 leads directly to a win for Player X, while Move 3 puts Player X at risk of losing. Move 2 is neutral.
Thus, we can evaluate these moves in terms of utility:
- Move 1: utility 1 (direct win)
- Move 2: utility 0 (neutral)
- Move 3: utility -1 (potential loss)
Clearly, the best option is Move 1.
Now, considering the previous turn, Player X has five options, none of which guarantee an immediate victory. How should Player X determine the optimal move? The selection hinges on Player O's response, which is unpredictable.
The move in the top right corner offers two chances for Player X to win in the next round:
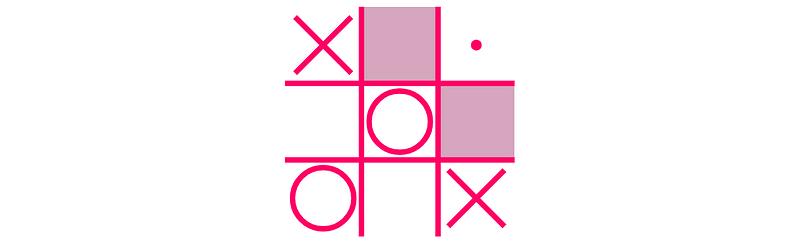
As Player O can only block one of these winning opportunities, Player X can secure a victory.
But what about Player X's opening move? The answer depends on Player O’s initial action, which in turn may be influenced by Player X's subsequent choice. This creates a complex web of decision-making.
Fortunately, there exists a systematic method to determine the best move in any scenario. Stay tuned for the next installment in our Game Theory series, where we will explore the Minimax algorithm.
Thank you for reading! If you wish to support Street Science, consider contributing on Patreon.