Chapter 1: A New Perspective on the Universe's Building Blocks

Most scientists today agree that the universe, including all of space, time, and matter, is fundamentally composed of fields. These fields, as far as current knowledge suggests, do not have a smallest indivisible element. This marks a significant shift away from the particle-centric view that dominated for centuries, yet there may still be an opportunity to revisit that perspective.

First, let's delve into some historical context:

Two millennia ago, philosophical debates on the nature of matter were prevalent. The Greek philosopher Aristotle believed all substances were made up of four elements—air, water, earth, and fire—and that matter could be subdivided indefinitely. In contrast, Democritus proposed that matter consists of minuscule, indivisible units called atoms.

Aristotle's influence was so profound that his views prevailed for centuries, overshadowing Democritus's ideas until the Enlightenment of the 18th century reignited interest in atomic theory. Thinkers such as Isaac Newton and Robert Boyle introduced new perspectives on matter, with Newton even proposing a "corpuscular" theory of light, foreshadowing the later discovery of photons. However, these ideas were largely speculative at the time.

It wasn't until the early 19th century that John Dalton laid the groundwork for atomic theory in a scientific context, which became the bedrock of modern chemistry. Around the same time, Avogadro advanced the understanding of how particles correlate with chemical ratios, leading to what is now known as Avogadro's number (approximately 6.022 x 10²³), representing the number of particles in a mole of substance.

The atomic model proved remarkably effective, as subsequent experiments continued to validate it. The discovery of subatomic particles like electrons and protons followed, and the development of particle accelerators in the early 20th century allowed scientists to collide particles and uncover even more.

With the advent of quantum mechanics, the notion of particles evolved to include wave characteristics, prompting a reevaluation of the particle model. If particles could also behave as waves, this suggested that they might resemble fields, aligning with Aristotle's original hypothesis. Depending on observation methods, they exhibited either wave or particle properties—a concept known as wave-particle duality.

So, did Aristotle have it right? Many physics texts suggest a dual affirmation, yet contemporary mathematical frameworks indicate a more decisive agreement with Aristotle's view, presenting challenges for physicists.

To address these complexities, physicists like Dirac, Feynman, and Schwinger in the 1930s and 40s developed quantum field theory (QFT) to describe the behavior of particles within accelerators, especially at velocities approaching light speed. QFT emerged as the gold standard for understanding matter, forces, and energy. It posits that both particles and waves are manifestations of underlying fields, with particles appearing when these fields possess the requisite energy.

However, the concept of "virtual particles," which are undetectable off-mass shell fields, complicates the interpretation of QFT, as they are mathematically "imaginary." This leads to a fundamental ontology where fields are the concealed reality, while particles are mere expressions of these fields in specific configurations.

This perspective was not universally accepted. David Bohm, who formulated Bohmian mechanics in the 1950s, and John Bell, who developed his renowned theorem on quantum probability, argued for a return to Democritus's ontology, positing that particles, not fields, represent the true essence of reality.

Bohm's approach, while intriguing, struggled to match the success of QFT, particularly in explaining the dynamics of high-speed particle collisions. In a bid to reconcile these theories, Bell crafted an alternative known as Bell-type Field Theories, where fields are understood as manifestations of numerous particles and their corresponding waves, with particles retaining their foundational significance.

To make this work, Bell and his contemporaries faced several challenges. Notably, QFT accounts for the creation and annihilation of particles in accelerators—an essential aspect of high-energy physics. Fields can easily generate new particles, given sufficient energy, while particle theories require a more explicit modeling of particle dynamics, including their creation and destruction.

In Bell-type field theories, particles are depicted as following "jump" trajectories—an abstract concept allowing particles to appear, traverse space, and then disappear. This peculiar behavior mirrors the quantum realm, where seemingly impossible events regularly occur.

For instance, consider quantum electrodynamics involving electrons, positrons, and photons. If two electrons interact to create a transient electron-positron pair, a perturbation term in field theory captures this interaction, often illustrated by a Feynman diagram.

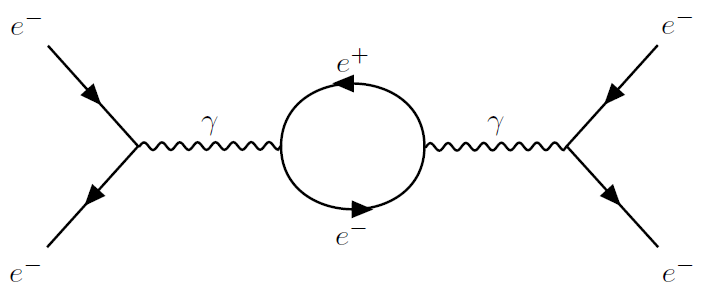
In contrast, a Bell-type field theory would require modeling each particle's trajectory over time. This entails tracking two incoming electrons, the emission of a photon, and the subsequent creation and annihilation of the electron-positron pair, culminating in the repulsion of the original electrons.

Ultimately, both Bell-type field theories and QFT yield similar predictions. Yet, QFT's reliance on unobservable virtual particles raises questions about the physical interpretation of these abstract mathematical constructs.

Chapter 2: Exploring Quantum Field Theory Through Visual Media

This video titled "QFT: What is the universe really made of? Quantum Field Theory visualized" delves into the intricacies of quantum field theory, exploring the fundamental constituents of the universe and how they interact through fields.

In "Tim Palmer: Non-Locality, Universe on a Fractal, Quantum Mechanics," the discussion centers on the non-local aspects of quantum mechanics and their implications for our understanding of the universe's structure.