Exploring Probability Generating Functions in Casino Games
Written on
Chapter 1: Understanding Probability Generating Functions
Imagine you are the owner of a Casino, and one of your most popular games is Craps. In this game, players roll two standard dice, and the objective is to achieve a total score ranging from 2 to 12. To enhance the experience for your patrons, you're considering introducing some exciting variations of this classic game.
One idea is to provide players with the option to choose between standard dice and "biased" dice. For instance, they could opt for a die marked with the numbers 1, 2, 2, 4, 5, and 6, alongside a regular die numbered 1 through 6. While the score range remains the same, the probabilities associated with each total score may vary. As a Casino owner, it's crucial to understand these changes to ensure you're not losing money due to the altered odds from specific dice selections.
To tackle this issue, let me introduce you to a valuable mathematical tool: the probability generating function.
Section 1.1: What is a Probability Generating Function?
Let ( X ) represent a discrete random variable, such as the outcome of a dice roll. The probability generating function (PGF) of ( X ) is defined as a power series polynomial where the coefficient of the term with index ( n ) corresponds to the probability that ( X = n ). Mathematically, this is represented as follows:
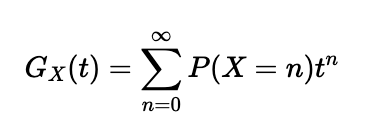
For instance, if ( X ) denotes the outcome of a fair six-sided die, where each side has an equal chance of landing face up, the PGF is established as:
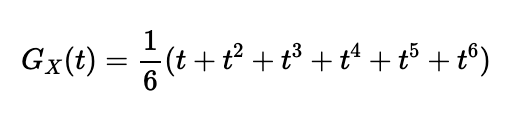
Probability generating functions possess several intriguing properties.
First, evaluating the function at ( t = 0 ) yields ( P(X = 0) ):
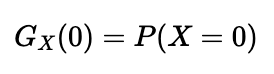
Second, evaluating the function at ( t = 1 ) provides the sum of the probabilities of all potential outcomes, which naturally equals 1:
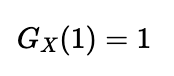
Third, you can derive ( P(X = k) ) from the function by differentiating it ( k ) times and then setting ( t=0 ):
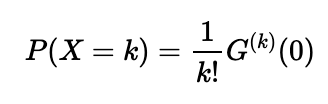
A noteworthy implication of this is that if two random variables share the same PGF, they will also exhibit the same probability mass function, meaning their outcome probabilities are identical. This principle is particularly significant for casino operators.
Fourth, in line with probability laws, if you have two independent events represented by discrete random variables, the PGF for the combined outcome is the product of their respective PGFs. Thus, for independent random variables ( X ) and ( Y ):
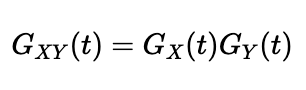
Finally, by differentiating our PGF once and setting ( t = 1 ):
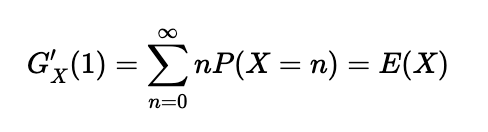
This allows us to easily calculate the expected value from the PGF.
Section 1.2: Enhancing the Game with PGFs
Now, let's revisit the PGF for a standard die, and decompose it into simpler polynomials for further exploration:
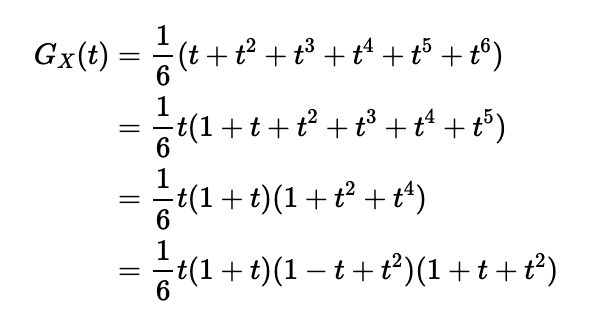
In a typical game of Craps, the total score results from rolling two independent dice. Therefore, the PGF for the sum of two standard dice can be calculated as the square of the PGF for a single die:
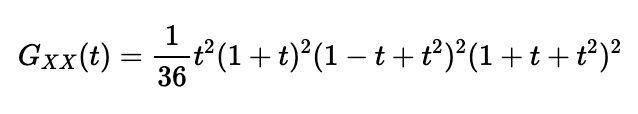
Next, let's explore the possibility of decomposing this function into two distinct valid PGFs whose product remains unchanged:
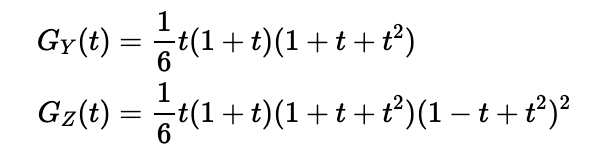
It's essential to confirm that these functions meet the necessary conditions:
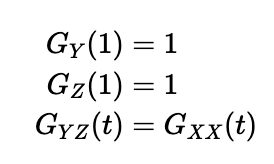
Let’s expand our newly defined functions to investigate whether they can identify two different dice suitable for our revamped Craps game. Expanding the first function yields:
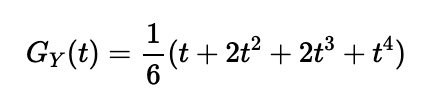
This generates a PGF for a die with faces numbered 1, 2, 2, 3, 3, and 4. For the second function, we derive:
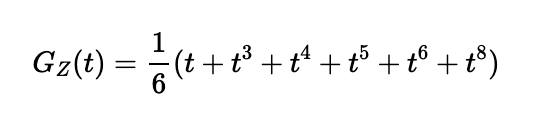
This results in a PGF for a die with faces numbered 1, 3, 4, 5, 6, and 8. Thus, as a casino owner, you can confidently offer an alternative pair of dice labeled 1, 2, 2, 3, 3, 4 and 1, 3, 4, 5, 6, 8 without affecting the game's odds.
Chapter 2: Another Example with Tetrahedral Dice
Imagine a game that involves rolling two tetrahedral dice, each marked with the numbers 1, 2, 3, and 4 (where the outcome is the visible side). The PGF for this random variable is:
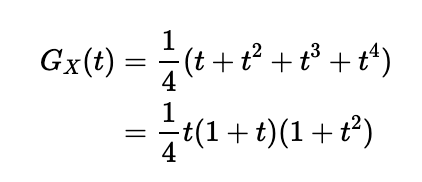
For two identical tetrahedral dice, the function for the total score would be:
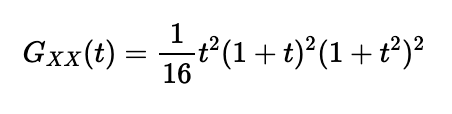
An alternative decomposition into two valid PGFs is as follows:
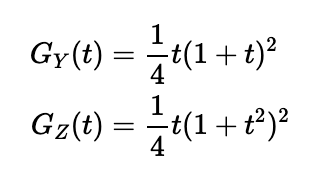
Upon expanding these functions, we discover that our dice can be substituted with two dice marked 1, 2, 2, 3 and 1, 3, 3, 5, all without changing the game's odds.
Special thanks to Archie Smith for presenting a problem that inspired this article. If you found any part of this discussion intriguing, please feel free to share your thoughts.
This video, "Probability Generating Functions - Worked Example," provides an in-depth look at how to effectively utilize PGFs in practical scenarios.
In this video, "SOA Exam P Question 211 | Hypergeometric Probability," learn how to solve complex probability problems related to PGFs.