Daily Scientific Challenge

At the core of quantum mechanics lies the renowned Heisenberg Uncertainty Principle, a fundamental concept that dictates the limits of precision in measuring quantum states:

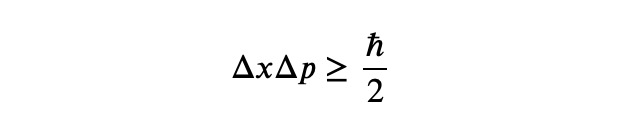
The "h bar" featured on the right represents Planck's constant, while ?? and ?? signify the uncertainties in a particle's position and momentum, respectively. The principle states that enhanced knowledge of one quantity leads to diminished knowledge of the other. Importantly, this is not merely a theoretical assertion! At atomic scales, any form of measurement inevitably disturbs the system, enforcing this limitation on uncertainties. Although the uncertainty principle is not a direct calculation tool, it underpins all phenomena at the quantum level. Today, your objective is to derive a lower limit for the quantum ground state of the harmonic oscillator.

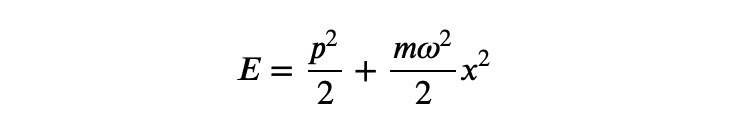
In this context, ?n is a positive integer, while ?, ?_0 are positive real constants. It's worth noting that in classical physics, the minimum energy would be ?=0, when both ? and ? are equal to zero. However, due to the Heisenberg uncertainty principle, achieving exact values for both quantities is impossible.

Implementing a Solution with Python

As is customary in SymPy, we initiate by defining our symbols:

The Heisenberg uncertainty relation can be expressed as:

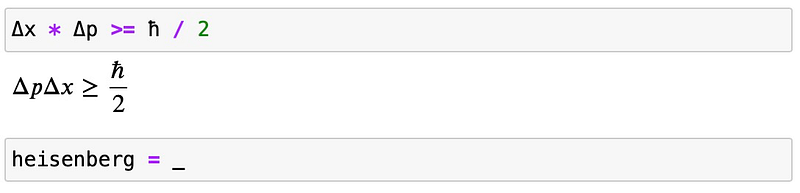
For the harmonic oscillator, we can represent it as:

Next, we will apply the uncertainty relation to substitute the position uncertainty:

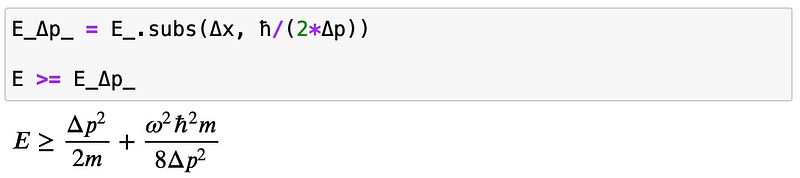
To find a lower bound for the energy, we seek the minimum and set the requirement:

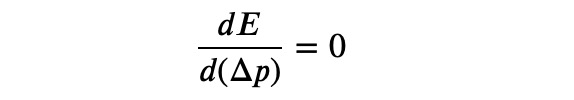
Continuing, we will solve for ??:

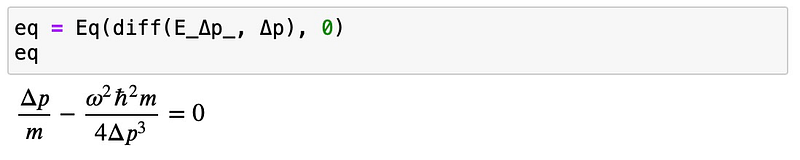
This results in the momentum uncertainty necessary to achieve minimum energy. We then substitute this value into our energy expression:

Ultimately, our conclusion is that the ground state energy must be at least ??/2. Remarkably, this is not just an estimation; it can be demonstrated that this represents the exact energy of the ground state.

Moving to a More General Potential

Now, let’s extend our findings to a broader potential scenario. We define the energy as follows:

By substituting the uncertainty relation:

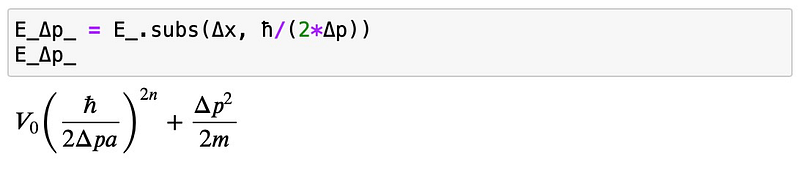
We will then investigate the minimum:

This time, we arrive at two potential solutions:

Since the uncertainty ?? must be positive, we can disregard the second solution.

Now, let’s insert the solution to ascertain the minimum energy:

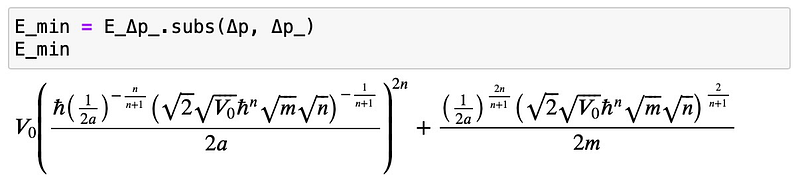
This scenario is relatively more complex, but by rearranging the terms for ?=1 (which simplifies to the harmonic oscillator case), we can observe the behavior as ?? approaches zero:

As ? represents the width of the potential, allowing ?? to approach zero leads to an increase in the minimum energy proportional to 1/?. In essence, confining the particle to a precise location results in a heightened uncertainty in momentum, subsequently raising the ground state energy of the system.

Relevant Videos

To deepen your understanding, check out these videos: